21-19 標準モルエントロピー

まず数式を元に熱容量をプロットする。

熱容量は T の多項式で表されている。(式の中に単位?→19-19 参照)

 ... (1)

エクセルの一番左の行に T を 0 ~ 1000 K まで 1 K 刻みで用意し、
上式の a, b, c, d を入力すれば C_P が表示されるようにしてみよう。

0~15 K はデバイの T³ 則を使う。(教科書p.900)

計算式の切り替わる温度 (15 K など)は行を2つ使って、前の計算式と後ろの計算式
(145.5 K なら固体の式と液体の式)の両方を計算している。

図示すると

熱容量 C_P はおおむね温度とともに増加していることがわかる。(振動エネルギーの影響→18-20参照)
液体領域は相転移前後の固体や気体に比べ、熱容量が大きい。

エントロピーの変化は C_P を T で割って積分すれば求められる。
(1)式を使えば

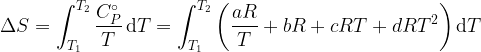
... (2)

(2)式の T₁ にはその式が有効な温度範囲の最初の温度(例えば15 K ~ 145.5 K なら 15 K) を、
T₂ には S を求めたい温度(エクセルの一番左の列の温度) を用いる。

(2)式は定積分なので、T₁ からの ΔS になっている。0 K からの S の絶対値を求めたいので、
前の式で計算した最後の温度 (例えば 15 K) での S を加える。

この操作は計算式の温度範囲が切り替わるたびに行う。
145.5 K では 固体→液体 の相転移が起こるので、相転移に伴う エントロピー変化分も加える。

240.3 K でも同様の操作を行う。

得られた S を図示すると次のようになる。

上記の昇温操作は全て 1 bar で行われているので、上図がシクロプロパンの標準モルエントロピーとなる。
テーブルなどに与えられている 25°C の標準モルエントロピーは 上図青線の 298.15 K の値 237.2 J K⁻¹ mol⁻¹ である。(非理想性の補正 0.54 J K⁻¹ mol⁻¹ を加えるとより正確になる。)

相転移温度で不連続に S が増加している所に注意してほしい。これは相転移に伴う熱の吸収によるもので、ジャンプ幅は 融解時より蒸発時の方が大きい。
(グラフでは、ここを垂直な縦線でつないでも良い。)

下記にエクセルファイルを置くが、これは参考として、
ぜひ自力でグラフを描画できるよう挑戦してもらいたい。

21-19.xlsx